Using Ambiguity, Contradiction, and Paradox to Create Mathematics

4.3 out of 5
| Language | : | English |
| File size | : | 3163 KB |
| Text-to-Speech | : | Enabled |
| Screen Reader | : | Supported |
| Enhanced typesetting | : | Enabled |
| Print length | : | 425 pages |
Mathematics is often perceived as a rigid and precise discipline, governed by strict rules and logical deductions. However, beneath this seemingly impenetrable exterior lies a hidden world of ambiguity, contradiction, and paradox. These concepts, often viewed as obstacles in other fields, play a vital role in mathematical discovery and innovation.
In the book "Using Ambiguity, Contradiction, and Paradox to Create Mathematics," author [Author's Name] delves into the fascinating intersection of these three concepts and their profound impact on mathematical progress. Through a series of compelling case studies and thought-provoking insights, the book explores how ambiguity, contradiction, and paradox can fuel creativity, inspire new solutions, and ultimately lead to groundbreaking mathematical breakthroughs.
Ambiguity: Embracing Uncertainty
Ambiguity is inherent in many mathematical problems. Situations where multiple interpretations or perspectives exist can create uncertainty or confusion. However, rather than being a hindrance, ambiguity can stimulate creative thinking and foster innovation.
For example, the concept of infinity has perplexed mathematicians for centuries. Its ambiguous nature, with its apparent contradictions and paradoxes, has sparked intense debates and led to the development of new mathematical theories and concepts.
Contradiction: Challenging Established Beliefs
Contradictions, statements that appear to be mutually exclusive or logically inconsistent, can be a source of great frustration in mathematics. However, when approached with an open mind, contradictions can become catalysts for new discoveries.
One famous example is the Banach-Tarski paradox, which asserts that a solid ball can be cut into a finite number of pieces and reassembled into two balls of the same size as the original. This seemingly paradoxical result forced mathematicians to rethink their fundamental assumptions about sets and volumes.

Paradox: Embracing the Unexpected
Paradoxes, statements that appear to be true yet lead to absurd or contradictory s, can challenge our deepest intuitions and force us to re-examine our understanding of the world.
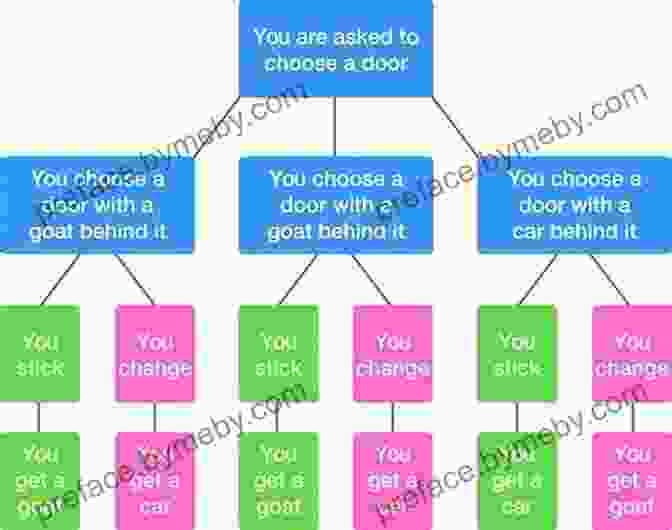
The famous Monty Hall problem is a classic example of a mathematical paradox. It presents a seemingly simple scenario but leads to an unexpected and counterintuitive result, which has sparked discussions and debates among mathematicians, statisticians, and philosophers.
Using Ambiguity, Contradiction, and Paradox to Create Mathematics is a groundbreaking work that challenges the traditional view of mathematics as a rigid and sterile discipline. Through its exploration of the interplay between these three concepts, the book provides a fresh perspective on the nature of mathematical discovery and innovation.
By embracing ambiguity, confronting contradictions, and grappling with paradoxes, mathematicians have pushed the boundaries of human knowledge and made extraordinary contributions to our understanding of the world we live in. This book is an essential read for anyone interested in the history, philosophy, and future of mathematics.
4.3 out of 5
| Language | : | English |
| File size | : | 3163 KB |
| Text-to-Speech | : | Enabled |
| Screen Reader | : | Supported |
| Enhanced typesetting | : | Enabled |
| Print length | : | 425 pages |
Do you want to contribute by writing guest posts on this blog?
Please contact us and send us a resume of previous articles that you have written.
 Book
Book Novel
Novel Page
Page Chapter
Chapter Text
Text Story
Story Genre
Genre Reader
Reader Library
Library Paperback
Paperback E-book
E-book Magazine
Magazine Newspaper
Newspaper Paragraph
Paragraph Sentence
Sentence Bookmark
Bookmark Shelf
Shelf Glossary
Glossary Bibliography
Bibliography Foreword
Foreword Preface
Preface Synopsis
Synopsis Annotation
Annotation Footnote
Footnote Manuscript
Manuscript Scroll
Scroll Codex
Codex Tome
Tome Bestseller
Bestseller Classics
Classics Library card
Library card Narrative
Narrative Biography
Biography Autobiography
Autobiography Memoir
Memoir Reference
Reference Encyclopedia
Encyclopedia Nevin Martell
Nevin Martell Mike Fallat
Mike Fallat Eric Butow
Eric Butow S Mark Young
S Mark Young Elaine N Aron
Elaine N Aron Ellen R Wald
Ellen R Wald Elizabeth May
Elizabeth May Tobe Melora Correal
Tobe Melora Correal Liane Holliday Willey
Liane Holliday Willey Julia Galef
Julia Galef Keith Giffen
Keith Giffen Ellyn Sanna
Ellyn Sanna Robert B Cialdini
Robert B Cialdini Jerry Pook
Jerry Pook Emily Suzanne Clark
Emily Suzanne Clark Elsa Sjunneson
Elsa Sjunneson Frank Murphy
Frank Murphy Elizabeth Kaledin
Elizabeth Kaledin Eric Schlosser
Eric Schlosser Emily Millikan Blair
Emily Millikan Blair
Light bulbAdvertise smarter! Our strategic ad space ensures maximum exposure. Reserve your spot today!

 Edgar Allan PoeAn Essay About Growing Up Jewish: A Journey of Identity, Faith, and Belonging
Edgar Allan PoeAn Essay About Growing Up Jewish: A Journey of Identity, Faith, and Belonging Nikolai GogolFollow ·19.5k
Nikolai GogolFollow ·19.5k J.R.R. TolkienFollow ·14k
J.R.R. TolkienFollow ·14k Elton HayesFollow ·3.1k
Elton HayesFollow ·3.1k Felipe BlairFollow ·16.4k
Felipe BlairFollow ·16.4k Jordan BlairFollow ·5.7k
Jordan BlairFollow ·5.7k Devin RossFollow ·8.7k
Devin RossFollow ·8.7k Vladimir NabokovFollow ·2.5k
Vladimir NabokovFollow ·2.5k Gene SimmonsFollow ·6.5k
Gene SimmonsFollow ·6.5k

 Richard Adams
Richard AdamsGame Development with Rust and WebAssembly: A...
Are you passionate...

 David Baldacci
David BaldacciGendered Identity and Aspiration on the Globalized Shop...
: The Convergence of Gender, Identity, and...

 Natsume Sōseki
Natsume SōsekiFresh Eyes On Panama: A Captivating Exploration of a...
Panama, a country often overshadowed by its...

 Adrian Ward
Adrian WardThe Life and Masterworks of J.M.W. Turner: A Timeless...
The Man Behind the Masterpieces ...
4.3 out of 5
| Language | : | English |
| File size | : | 3163 KB |
| Text-to-Speech | : | Enabled |
| Screen Reader | : | Supported |
| Enhanced typesetting | : | Enabled |
| Print length | : | 425 pages |














